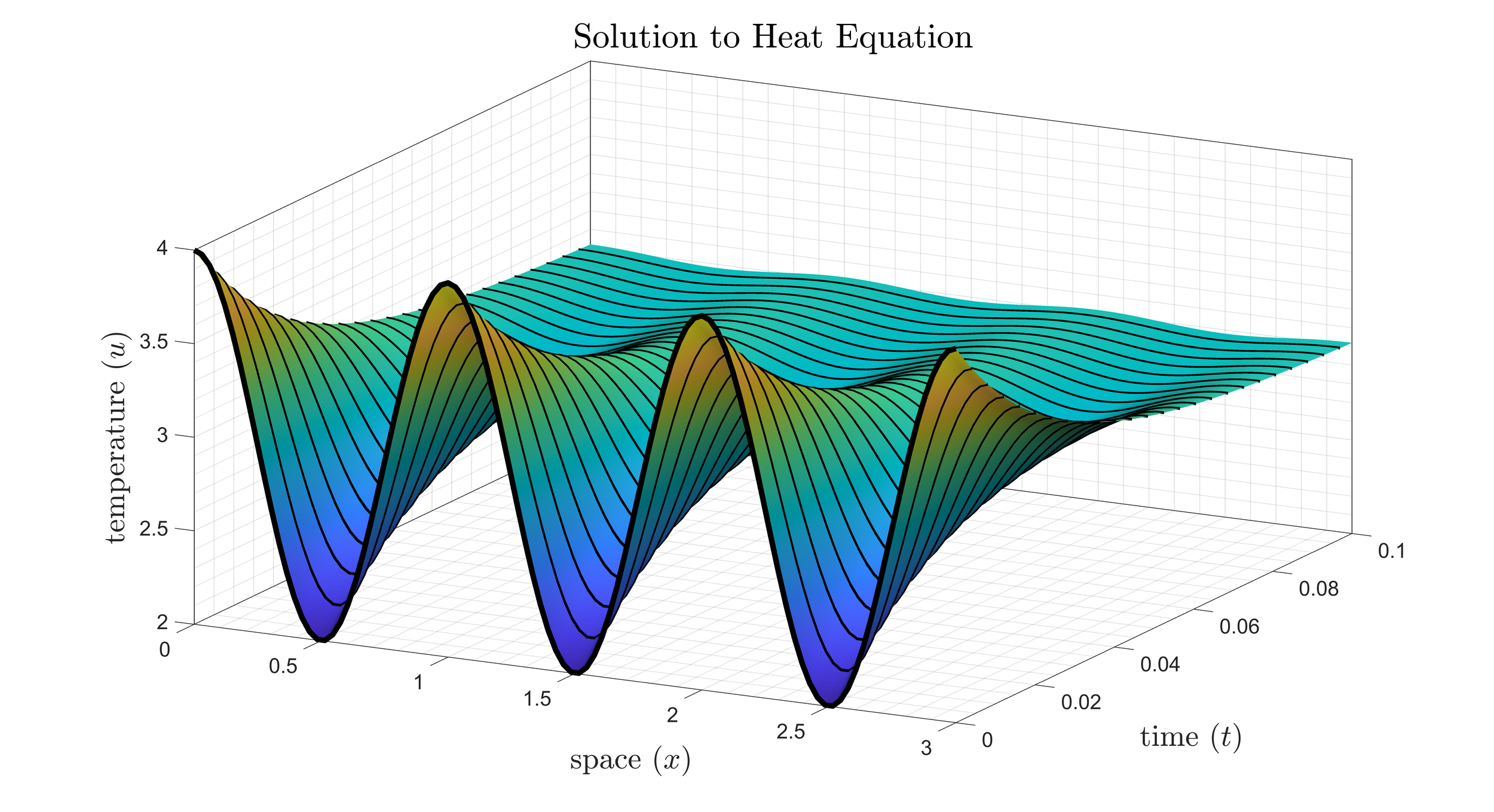
MAT 473 -- Partial Differential Equations
This course is an introduction to the theory of and solutions to partial differential equations. The three big PDEs are the motivation: the heat equation, the wave equation, and Laplace’s equation. A solid understanding of linear systems of IVPs is assumed, and a strong focus on BVPs and Cauchy-Euler problems is applied initially. The theory and application of Fourier Series is motivated by finding the solutions to the three PDEs with Dirichlet and/or Neumann boundary conditions. Solutions of nonhomogeneous PDES on finite domains are considered as well as integral transforms for semi-infinite and infinite domain problems. Other topics include the method of characteristics, existence theorems, and Green’s Functions. The figure depicts the solution to the heat equation with no flux boundary conditions.
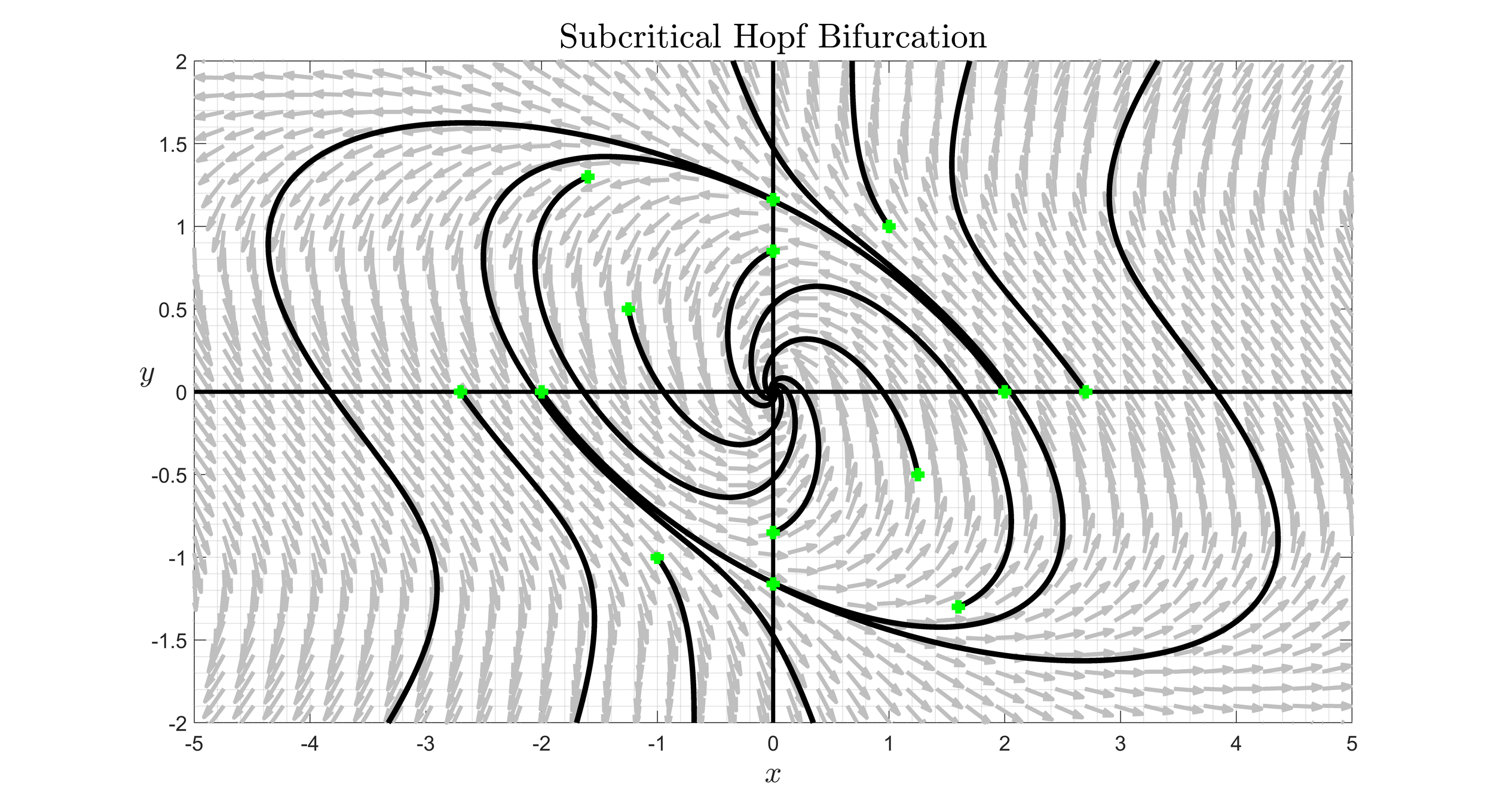
MAT 340 -- Differential Equations
An introduction to the theory of ordinary differential equations and their applications. Topics include analytical and qualitative methods for analyzing first-order differential equations, second-order differential equations, and systems of differential equations with an emphasis on modeling predator-prey and competing species systems. Analytical methods for finding solutions to differential equations will range from separation of variables and variation of parameters to Laplace transforms. Special emphasis will be placed on equilibria, stability analysis, and phase portraits of both linear and nonlinear equations and systems. The figure shows the phase-portrait with several trajectories of a nonlinear system that undergoes a subcritical Hopf bifurcation.
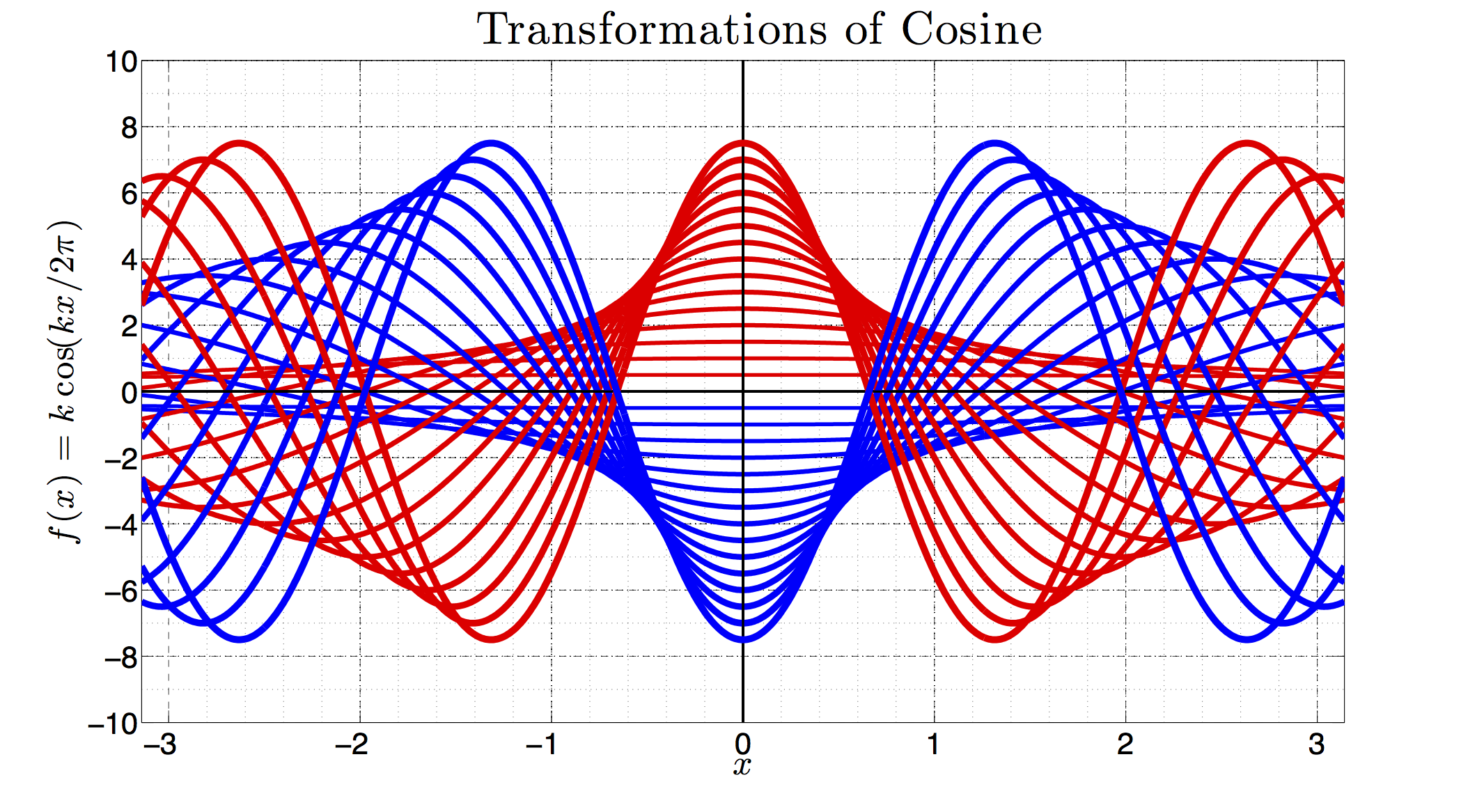
MAT 106 -- Trigonometry
This course is intended for students with an elementary knowledge of algebra who need more work in trigonometric topics before taking more advanced mathematics courses. Topics include properties of and operations of functions, inverse functions, exponential and logarithmic functions, angle measurement, trigonometric functions and their inverses, graphing functions, and problem solving with equations. The figure shows the graph of the cosine function for increasing amplitude and increasing frequency given by f(x) = kcos(kx/2pi), for k ranging from -15 to 15.


